Introducción a Ramda.js - Parte 0

En esta serie vamos a aprender programación funcional utilizando Ramda, una librería de JavaScript que nos entrega utilidades para realizar programación libre de efectos secundarios por medio de funciones puras.

Puedes ver todos los artículos en la serie a continuación

• Introducción a Ramda.js - Parte 0 (este mismo artículo☝️)

En este artículo vamos a revisar algunos conceptos básicos y terminología necesaria para entender la filosofía detrás de Ramda.

Este artículo fue publicado originalmente aquí

Funciones puras y efectos colaterales

Las funciones puras cumplen con 3 reglas:

• Para un mismo input siempre retornan el mismo output
• Poseen transparencia referencial (una función pura puede ser reemplazada por su resultado)
• No producen efectos colaterales

El objetivo principal al hacer programación funcional es encapsular lógica componiendo funciones puras y reducir el área en un programa donde se producen los efectos colaterales.

La ventaja de hacer esto es que al extraer los efectos secundarios de las transacciones lógicas de un programa, es mucho más fácil probar dichas transacciones y hacerlas predecibles, pues las funciones sólo dependen de sus inputs. Igualmente el área de superficie de un programa donde se producen side effects está contenida, por lo que también es más fácil razonar sobre dichos efectos y testearlos.

Un side effect o efecto colateral/secundario se refiere a una modificación de cualquier tipo de estado en un programa: desde cambiar el valor de una variable a hacer una petición http y cualquier cosa entre medio.

Todas las funciones expuestas por Ramda son funciones puras, por lo que carecen de efectos secundarios. Igualmente, todas las funciones están automáticamente curriadas. ¿Qué significa esto en estricto rigor?

Currying

Currying es un mecanismo que nos permite aplicar (invocar) una función f con una cantidad parcial de argumentos y obtener de vuelta una función g que espera el resto de los argumentos que no le pasamos a f. Por ejemplo:

// addSeveralNumbers es una función curriada que suma
// los 6 parámetros que recibe
const addSeveralNumbers = (a, b, c, d, e, f) => { /* ... */ }

const addAllButFirst = addSeveralNumbers(1);
const addRemainingTwo = addSeveralNumbers(1, 2, 3, 4);

addAllButFirst(2, 3, 4, 5, 6) === addRemainingTwo(5, 6) // true

Al definir addAllButFirst hemos aplicado addSeveralNumbers con sólo 1 argumento, por lo que addAllButFirst esa una función que espera los 5 parámetros restantes. En el caso de addRemainingTwo, hemos llamado a addSeveralNumbers con 4 argumentos, por lo que recibimos de vuelta una función con aridad 2.

Aridad es un término que se utiliza para describir la cantidad de argumentos que una función espera. Una función que espera un sólo argumento tiene aridad 1. En nuestro casoaddSeveralNumbers tiene aridad 6, pues espera seis argumentos.

Una implementación simplificada de addSeveralNumbers sería:

const addSeveralNumbers = a => {
  return b => {
    return c => {
      return d => {
        return e => {
          return f => {
            return a + b + c + d + e + f;
          }
        }
      }
    }
  }
};

O utilizando el return implícito de las funciones flecha:

const addSeveralNumbers = a => b => c => d => e => f =>  (a + b + c + d + e + f);

Desafortunadamente nuestra implementación nos limita a llamar cada función con un sólo argumento, por lo que nuestra definición de addRemainingTwo quedaría así:

const addRemainingTwo = addSeveralNumbers(1)(2)(3)(4);

Recordemos que addSeveralNumbers recibe sólo un parámetro y retorna una función. Esa función igualmente recibe sólo un parámetro y retorna otra función, y así sucesivamente cada función recibe un parámetro y retorna otra función hasta llegar a la última función que recibe el parámetro f y retorna la suma de a, b, c, d, e y f.

addSeveralNumbers(1)(2)(3)(4)(5)(6); // 21
//| 1 => ...etc  --|
//|-- 2 => ...etc  ---|
//|---- 3 => ...etc  ----|
//|------ 4 => ...etc  -----|
//|-------- 5 => ...etc  ------|
//|---------- 6 => 1 + 2 + 3 + 4 + 5 + 6;

Afortunadamente Ramda incluye una función curry para convertir funciones comunes y corrientes en funciones curriadas y así poder realizar aplicación parcial de mejor forma:

import { curry } from 'ramda';

const addSeveralNumbers = curry((a, b, c, d, e, f) => {
  return a + b + c + d + e + f;
});

Y luego:

addSeveralNumbers(1, 2, 3, 4, 5, 6) // 21
addSeveralNumbers(1, 2, 3, 4)(5, 6) // 21
addSeveralNumbers(1)(2, 3, 4, 5, 6) // 21
addSeveralNumbers(1)(2)(3)(4)(5)(6) // 21

¡Mucho mejor!

¿Cuándo es útil el currying?

Entendamos lo utilidad del currying a través de un ejemplo. Para efectos demostrativos, digamos que tenemos que implementar nuestra propia versión de Array.prototype.map. Podríamos hacerlo de la siguiente manera:

function map(projectionFn, arr) {
  const result = [];

  for (const item of arr) {
    result.push(projectionFn(item));
  }

  return result;
}

En este caso aplicamos la función de proyección projectionFn a cada elemento de nuestro arreglo inicial (sin mutarlo), retornando un nuevo arreglo:

map(x => x * 2, [1, 2, 3, 4]); // [2, 4, 6, 8]

Si quisiéramos aplicar la misma función para múltiples arreglos, podríamos hacer algo por el estilo:

const timesTwo = x => x * 2;

map(timesTwo, [1, 2, 3, 4]); // [2, 4, 6, 8]
map(timesTwo, [4, 2]);       // [8, 4]
map(timesTwo, [1, 1, 1, 3]); // [2, 2, 2, 6]
map(timesTwo, [5, 7, -3]);   // [10, 14, -6]

Podemos notar que para cada llamada a map le pasamos timesTwo como primer parámetro. Nuestro código podría quedar más legible si hiciéramos algo como:

const timesTwo = x => x * 2;

const mapTimesTwo = arr => {
  return map(timesTwo, arr);
};

mapTimesTwo([1, 2, 3, 4]); // [2, 4, 6, 8]
mapTimesTwo([4, 2]);       // [8, 4]
mapTimesTwo([1, 1, 1, 3]); // [2, 2, 2, 6]
mapTimesTwo([5, 7, -3]);   // [10, 14, -6]

Desafortunadamente si también quisiéramos implementar una función que multiplica cada elemento de nuestro arreglo por 3, tenemos que duplicar la misma lógica, salvo que sólo cambiando la función que le pasamos a map internamente:

const timesTwo = x => x * 2;
const timesThree = x => x * 3;

const mapTimesTwo = arr => map(timesTwo, arr);
const mapTimesThree = arr => map(timesThree, arr);

Podemos resolver este problema haciendo de map una función curriada:

import { curry } from 'ramda';

const map = curry((projectionFn, arr) => {
  const result = [];

  for (const item of arr) {
    result.push(projectionFn(item));
  }

  return result;
});

Y luego re-implementamos mapTimesTwo:

const timesTwo = x => x * 2;
const fn = map(timesTwo);

const mapTimesTwo = arr => fn(arr);

Fijémonos que const mapTimesTwo = arr => fn(arr) es idéntico a simplemente const mapTimesTwo = fn.

Si no te queda claro, quizás es más simple verlo así:

const log = message => console.log(message);

log('foo'); // "foo"
console.log('foo'); // "foo"

En este caso, log es una función que recibe un parámetro message y llama a la función console.log pasándole el mismo parámetro. ¿Qué diferencia tiene llamar a log o directamente a console.log? Para este caso puntual, ninguna. log es sólo un alias de console.log, por lo que podríamos definirla del siguiente modo:

const log = console.log;

Aplicando esto en nuestro ejemplo inicial:

const timesTwo = x => x * 2;
const timesThree = x => x * 3;

const mapTimesTwo = map(timesTwo);
const mapTimesThree = map(timesThree);

mapTimesTwo([1, 2, 3, 4]); // [2, 4, 6, 8]
mapTimesTwo([4, 2]);       // [8, 4]
mapTimesThree([1, 2, 3]);  // [3, 6, 9]
mapTimesThree([5, 7]);     // [15, 21]

¡Mucho mejor! Y todo gracias al currying.

Point-free style

La forma en la que acabamos de escribir nuestras funciones se conoce como estilo sin argumentos o point-free style. Gracias al currying y a que nuestras funciones reciben como último argumento la data sobre la que operan, podemos hacer aplicación parcial de funciones sin declarar el argumento final. Todas las funciones en Ramda siguen este principio y nos da pie a escribir código declarativo de forma directa y legible. Retomemos nuestro ejemplo:

import { map } from 'ramda';

const mapTimesTwo = arr => map(x => 2 * x, arr);

Reescribiremos esta función paso a paso utilizando point-free style:

import { map, multiply } from 'ramda';

const mapTimesTwo = arr => map(x => multiply(2, x), arr);

Como multiply es una función curriada, x => multiply(2, x) es lo mismo que decir x => multiply(2)(x) y por lo tanto, idéntico a multiply(2):

import { map, multiply } from 'ramda';

const mapTimesTwo = arr => map(multiply(2), arr);

Y como map también está curriada, arr => map(fn, arr) es equivalente a arr => map(fn)(arr), y por lo tanto idéntico a map(fn). Finalmente obtenemos:

import { map, multiply } from 'ramda';

const mapTimesTwo = map(multiply(2));
mapTimesTwo([1, 2, 3, 4]); // [2, 4, 6, 8]

Esto queda claramente más directo y fácil de leer que cualquier de nuestros ejemplos anteriores. Como Ramda igualmente posee definiciones de tipos para TypeScript, podemos obtener muy buena inferencia de tipos en IDEs como VSCode de forma gratuita (sin necesidad de utilizar TypeScript en nuestro proyecto).

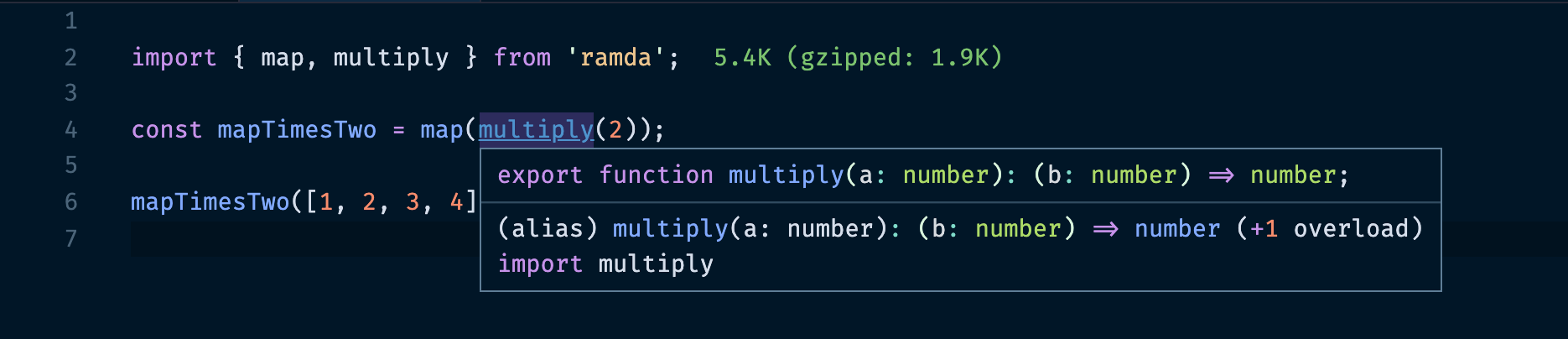
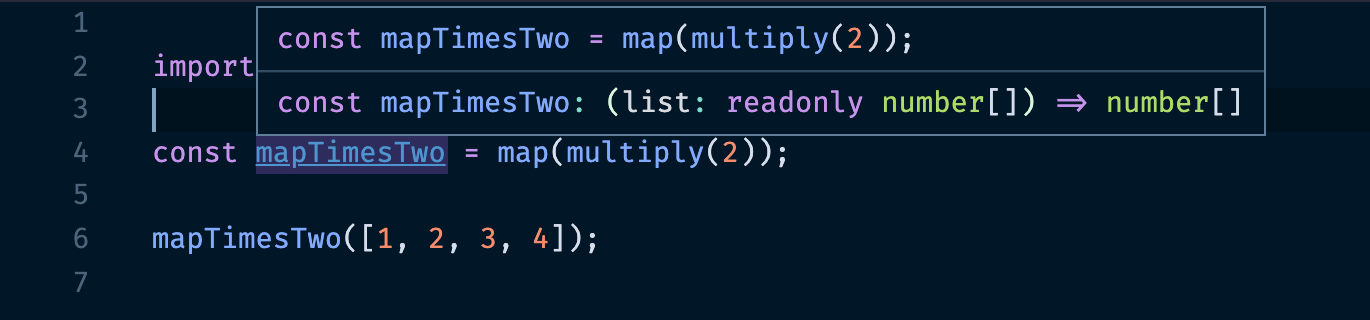
En este caso VSCode nos informa que mapTimesTwo es una función que toma como parámetro un arreglo de números y retorna otro arreglo de números. El tipo de elementos del arreglo (number) es inferido a partir de la función multiply(2), que retorna una función que espera recibir un número y retornar otro número.

Inmutabilidad

Finalmente, hablemos de inmutabilidad.

Al hacer programación funcional es muy importante que trabajemos nuestra data de forma inmutable. Una estructura de datos es inmutable cuando, para representar un cambio de estado, no alteramos la estructura en sí, si no que derivamos una nueva estructura de datos a partir de la original.

Mantener la inmutabilidad en nuestros programas aumenta la previsibilidad de cómo va cambiando el estado, ya que cada cambio de estado es explícito.

Al tratar los cambios de estado de forma explícita, podríamos incluso rastrearlos y generar un sistema de navegación entre los distintos estados de un programa, también conocido como time traveling debugging.

Está de más decir que todas las funciones expuestas por Ramda, tratan sus argumentos de forma inmutable.

Eso ha sido todo por hoy. Si te ha gustado el contenido, no te olvides de darle una compartida en Twitter. En el próximo artículo vamos a hablar de composición de funciones.

Gracias totales y hasta la próxima.